[ 문제 ]
19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.
택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.
D(T1,T2) = |x1-x2| + |y1-y2|
두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.
따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.
원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합
반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을 작성하시오.
[ 코드 ]
StreamReader sr = new StreamReader(Console.OpenStandardInput());
StreamWriter sw = new StreamWriter(Console.OpenStandardOutput());
int n = int.Parse(sr.ReadLine());
double a = Math.PI * n * n;
double b = 2 * n * n;
sw.Write($"{a:F6}\n{b:F6}");
sw.Flush();
sw.Close();
sr.Close();
[ 추가 ]
유클리드 기하학으로 원의 넓이 구하는 방법은 우리가 기본적으로 알고있는 파이*반지름의 제곱으로 구하면 되고,
택시 기하학은 비유클리드 기하학으로 분류되며 수직이나 수평으로만 움직여서 값을 구하는 것이라고 한다.
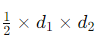
마름모의 공식을 이용한 택시 기하학 문제 풀기.
주어진 원에 사각형이 내접해있다고 하면 원의 지름이 사각형의 대각선 길이가 된다.
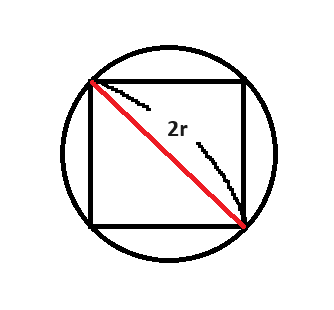
마름모의 공식은 R * R / 2 를 하는것이기에 문제에 주어진 반지름(r)에 2씩 곱해줘 2r(=R)로 만들어준다.
그렇게 되면 (2r * 2r) / 2가 되는데 그럼 4r^2 / 2라서 2r^2으로 풀어주면 된다.
https://ko.wikipedia.org/wiki/%EB%A7%A8%ED%95%B4%ED%8A%BC_%EA%B1%B0%EB%A6%AC
맨해튼 거리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 맨해튼 거리와 유클리드 거리의 비교: 맨해튼 거리인 빨간색, 파란색, 노란색 선의 길이는 모두 12이며 가장 짧은 맨해튼 거리이다. 유클리드 거리인 초록색 선
ko.wikipedia.org
[ 실행화면 ]

문제링크: https://www.acmicpc.net/problem/3053
3053번: 택시 기하학
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
www.acmicpc.net
'Language > C#' 카테고리의 다른 글
| [C#] 백준 7510번 고급 수학 (0) | 2024.04.04 |
|---|---|
| [C#] 백준 3034번 앵그리 창영 (0) | 2024.04.03 |
| [C#] 백준 10569번 다면체 (오일러의 다면체 정리) (0) | 2024.04.03 |
| [C#] 백준 N과 M (1) (백트래킹 재귀함수) (0) | 2024.04.02 |
| [C#] 백준 1931번 회의실 배정 (0) | 2024.04.02 |